Skip to content

S2OJ - 1426. 空

题解969 字
# 2022 # S2OJ # STL
检测到 KaTeX 加载失败，可能会导致文中的数学公式无法正常渲染。

#题面

#题目描述

Utsuho 有 nn 条线段，现在她希望在其中找到两条有公共点的线段，使得它们的异或值最大。

定义线段异或值为它们并的长度减它们交的长度。

#输入格式

输入的第一行包括一个正整数 nn，表示 Utsuho 的线段的个数。

接下来 nn 行每行包括两个正整数 l,rl, r，表示 Utsuho 拥有的线段的左右端点。

#输出格式

输出一行一个整数，表示能得到的最大异或值。

#输入输出样例

样例输入 #1

3
10 100
1 50
50 100

样例输出 #1

99

样例解释 #1

  • 选择第一条和第二条：99−40=5999 - 40 = 59；
  • 选择第一条和第三条：90−50=4090 - 50 = 40；
  • 选择第二条和第三条：99−0=9999 - 0 = 99。

样例输入 #2

3
1 100
180 200
190 210

样例输出 2

20

#数据规模与约定

  • 对于 20%20\% 的数据，满足 l,r,n≤300l, r, n \le 300;
  • 对于 40%40\% 的数据，满足 n≤2×103n \le 2 \times 10^3;
  • 另有 10%10\% 的数据，满足 l=1l = 1;
  • 对于 100%100\% 的数据，满足 1≤n≤2×1051 \le n \le 2 \times 10^5，1≤l≤r≤1081 \le l \le r \le 10^8。

#思路

算是个优化版的暴力。考场上的思路不是特别清晰，所以前前后后一共搞了一个多小时。这个做法的不如正解的简单明了，但是跑的比正解快，内存占用还比正解小。

同一直线上的两条线段存在一下几种关系：

  1. 包含，两者的异或值为 (l2−l1)+(r1−r2)(l_2 - l_1) + (r_1 - r_2)；
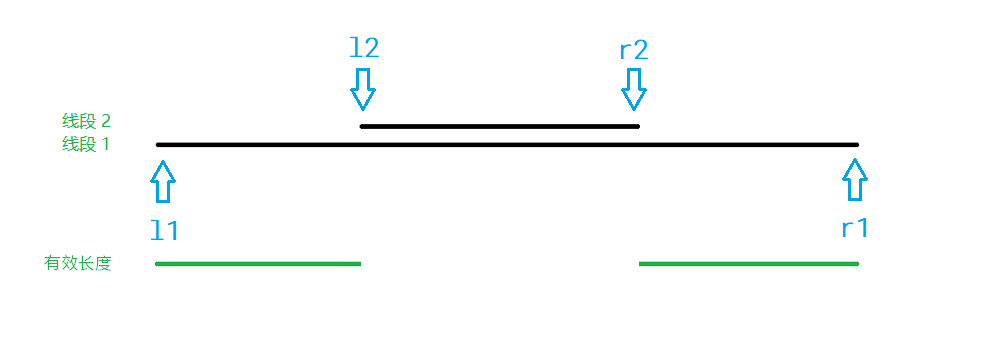
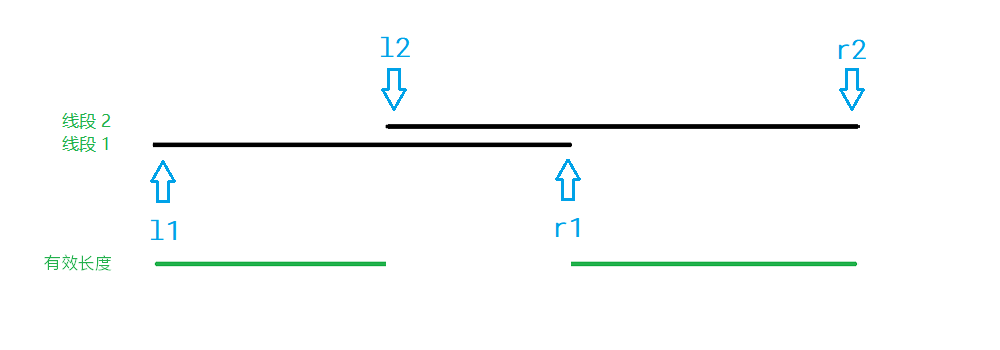
  2. 相交，两者的异或值为 (l2−l1)+(r2−r1)(l_2 - l_1) + (r_2 - r_1)；
  3. 相离，此时对最大异或值没有贡献，忽略即可。

接下来可以分类讨论：

  1. 对于包含的情况，可以枚举线段 2，然后使用堆维护前面所有线段中长度最长的线段作为线段 1。
  2. 对于相交的情况，上方的计算异或值的式子可以改写为 (l2+r2)−(l1+r1)(l_2 + r_2) - (l_1 + r_1)，那么可以枚举线段 2，并使用堆维护 (l+r)(l + r) 值最大的线段 1。

可以使用优先队列模拟堆，省去了手写的麻烦。

#代码

C++
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
71
72
#include <algorithm>
#include <iostream>
#include <queue>
#include <utility>
#include <vector>

using std::cin;
using std::cout;
const char endl = '\n';

const int N = 2e5 + 5;

int n, ans;
std::pair<int, int> lines[N];

// 包含
std::priority_queue<
    std::pair<int, int>,
    std::vector<std::pair<int, int>>,
    auto(*)(std::pair<int, int>, std::pair<int, int>)->bool>
q1([](std::pair<int, int> a, std::pair<int, int> b) -> bool {
    return a.second - a.first < b.second - b.first;
});

// 相交
std::priority_queue<
    std::pair<int, int>,
    std::vector<std::pair<int, int>>,
    auto(*)(std::pair<int, int>, std::pair<int, int>)->bool>
q2([](std::pair<int, int> a, std::pair<int, int> b) -> bool {
    return a.first + a.second > b.first + b.second;
});

int main() {
    std::ios::sync_with_stdio(false);

    cin >> n;

    for (int i = 1; i <= n; i++) {
        cin >> lines[i].first >> lines[i].second;
    }

    std::sort(lines + 1, lines + 1 + n);

    q1.push(lines[1]);
    q2.push(lines[1]);

    for (int i = 2; i <= n; i++) {
        while (!q1.empty() && lines[i].second >= q1.top().second) q1.pop();  // 剔除已经相交的线段
        while (!q2.empty() && lines[i].first >= q2.top().second) q2.pop();   // 剔除已经相离的线段

        if (!q1.empty()) {
            auto p = q1.top(),
                 q = lines[i];
            ans = std::max(ans, (p.second - p.first) - (q.second - q.first));
        }

        if (!q2.empty()) {
            auto p = q2.top(),
                 q = lines[i];
            ans = std::max(ans, (q.second - p.second) + (q.first - p.first));
        }

        q1.push(lines[i]);
        q2.push(lines[i]);
    }

    cout << ans << endl;

    return 0;
}