S2OJ - 1461. 豌豆射手

#题面

#题目背景

愚蠢的戴夫种了一些豌豆射手。

愚蠢的戴夫只会把豌豆射手种在一列草坪上，并且因为戴夫不懂得种植向日葵，所以他并没有足够的阳光使得这一列都放满豌豆射手。

但这些豌豆射手除了会向前喷射豌豆，还会向左右喷射豌豆，并且向左右喷射豌豆有一个飞行距离限制。

一大波僵尸即将来临，戴夫想要知道，有多少种安排豌豆射手的方案，使得没有两个豌豆射手会相互攻击。

#题目描述

现在有 $n$ 个豌豆射手，要把它们放在长度为 $d$ 的一列草坪上。

每一个豌豆射手都有一个攻击半径 $r_i$，如果将这个豌豆射手放在 $\mathit{pos}$ 位置，那么 $[\mathit{pos} - r_i + 1, \mathit{pos} + r_i - 1]$ 将不能有其他的豌豆射手。

戴夫要把这 $n$ 个豌豆射手放在长度为 $d$ 的草坪上，使得它们不会相互攻击，求方案数。答案对 $10^9+7$ 取模

#输入格式

第一行两个整数 $n, d$，表示有 $n$ 个豌豆射手，草坪的长度为 $d$。

第二行 $n$ 个整数 $r_i$，表示每一个豌豆射手的攻击半径。

#输出格式

一行一个整数，表示合法的方案数。

#输入输出样例

样例输入 #1

4 4
1 1 1 1

样例输出 #1

24

样例输入 #2

3 47
4 8 9

样例输出 #2

28830

样例输入 #3

8 100000
21 37 23 13 32 22 9 39

样例输出 #3

923016564

#数据范围与约定

对于 $20\%$ 的数据，$n \leq 5$，$d \leq 14$；
对于 $60\%$ 的数据，$n \leq 18$；
对于 $100\%$ 的数据，$n \leq 40$，$d \leq 10^5$，$1 \leq r_i \leq 40$，$\sum_{i = 1}^{n}r_i \leq d$。

#思路

设豌豆射手的顺序为 $p_1, p_2, \dots, p_n$，设 $\displaystyle x = \sum_{i = 1}^{n} \max(r_{p_i}, r_{p_{i + 1}})$，则当前排列的方案数为 $\begin{pmatrix} d - x + n \\ n \end{pmatrix}$。那么问题就转变为了对于每一个 $x$ 有多少方案。

先将 $r_i$ 升序排序，设 $f_{i, j, k}$ 表示前 $i$ 个点中有 $j$ 个点的左右位置还可以放置豌豆射手（称为空闲点），放置后 $x$ 的大小为 $k$ 的方案。

初始值：$f_{0, 0, 0} = 1$，表示一开始一个点都没有，空闲点的数量也是 $0$，合并的长度也是 $0$ 的方案。

定义「合并」：表示将一个新的点和一个空闲点相连，那么新合成的这一段又可以看成一个空闲点。有以下几种情况：

1. 将当前点合并到某个空闲点的左右两边。

   

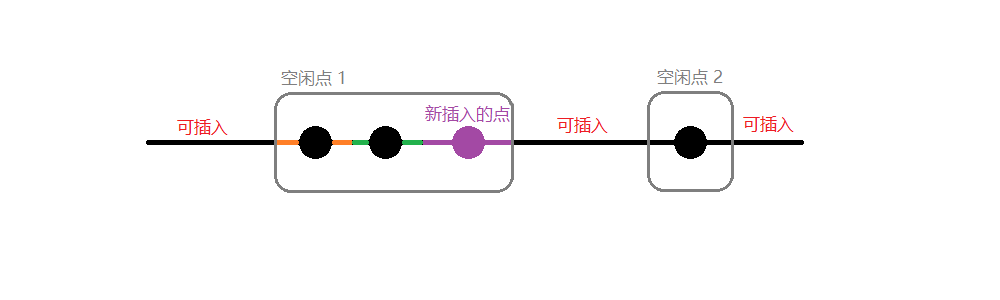
   此时空闲点的数量不变，长度加上新的点的半径。

   $$\large f_{i + 1,j + 1, k + r_{i + 1}} \leftarrow f_{i, j, k} \times j \times 2$$

   由于已经对 $r$ 进行过排序，所以 $r_{i + 1}$ 一定是 $r_{i}$ 和 $r_{i + 1}$ 中最大的那个，直接使用即可。

   式子中的乘 $j$ 是可以从 $j$ 个空闲点中挑出一个和新的点合并，乘以 $2$ 是可以放在左右两边。

2. 将当前点插入到两个空闲点的中间，使左右两个空闲点合并。

   

   此时空闲点的数量减 $1$，长度加上新半径乘以 $2$，因为往左右两边扩展，然后减去中间算重复的。

   $$\large f_{i + 1, j − 1, k + r_{i + 1} \times 2 − 1} \leftarrow f_{i, j, k} \times j (j − 1)$$

   因为这 $j$ 个空闲点具体位置在哪都是不确定的，选取出两个点左右关系也是不确定的，所以乘 $j(j - 1)$ 而不是除 $2$。

3. 单独成为一个空闲点。

   

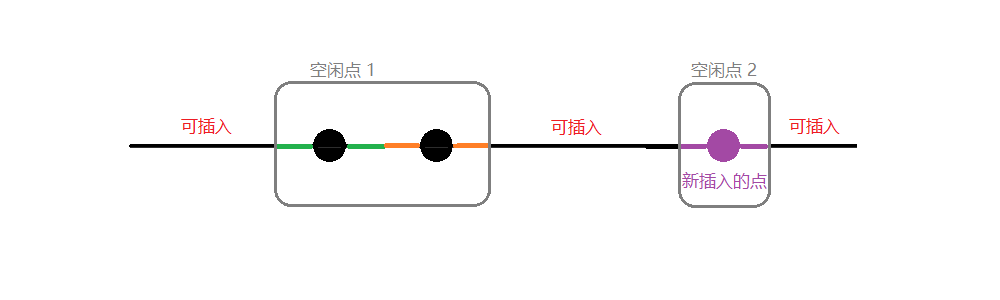
   此时空闲点的数量加 $1$，长度加 $1$。

   $$f_{i + 1, j + 1, k + 1} \leftarrow f_{i, j, k}$$

时间复杂度为 $O(n^3 \max\{r_i\})$。

#代码

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
71
72
73
74
75
76
77
78
79
80
81
82
83
84
85
86
87
88

#include <iostream>
#include <algorithm>

using std::cin;
using std::cout;
const char endl = '\n';

const int N = 45,
          D = 1e5 + 5;
const int mod = 1e9 + 7;

int n, d, r[N], f[N][N][N * N], max, ans;
int fac[D], inv[D];

int binpow(int a, int b) {
    int res = 1;
    a %= mod;
    while (b) {
        if (b & 1) res = 1ll * res * a % mod;
        a = 1ll * a * a % mod;
        b >>= 1;
    }
    return res;
}

inline int C(int n, int m) {
    return 1ll * fac[n] * inv[m] % mod * inv[n - m] % mod;
}

int main() {
    std::ios::sync_with_stdio(false);
    cin.tie(nullptr);

    // 阶乘
    fac[0] = 1;
    for (int i = 1; i <= 100000; i++) {
        fac[i] = 1ll * fac[i - 1] * i % mod;
    }

    // 逆元
    inv[0] = inv[1] = 1;
    for (int i = 2; i <= 100000; i++) {
        inv[i] = static_cast<long long>(mod - (mod / i)) * inv[mod % i] % mod;
    }

    // 阶乘的逆元
    for (int i = 2; i <= 100000; i++) {
        inv[i] = static_cast<long long>(inv[i - 1]) * inv[i] % mod;
    }

    cin >> n >> d;

    for (int i = 1; i <= n; i++) {
        cin >> r[i];

        max = std::max(max, r[i]);
    }

    std::sort(r + 1, r + 1 + n);

    f[0][0][0] = 1;

    for (int i = 0; i <= n; i++) {
        for (int j = 0; j <= i; j++) {
            for (int k = 0; k <= max * (i - j + 2); k++) {
                int t = r[i + 1];

                if (j >= 1) {
                    f[i + 1][j][k + t] = (f[i + 1][j][k + t] + 1ll * f[i][j][k] * 2 * j) % mod;
                }

                if (j >= 2 && k) {
                    f[i + 1][j - 1][k + t * 2 - 1] = (f[i + 1][j - 1][k + t * 2 - 1] + 1ll * f[i][j][k] * j * (j - 1)) % mod;
                }

                f[i + 1][j + 1][k + 1] = (f[i + 1][j + 1][k + 1] + f[i][j][k]) % mod;
            }
        }
    }

    for (int i = 0; i <= n * max; i++) {
        ans = (ans + 1ll * C(d - i + n, n) * f[n][1][i] % mod) % mod;
    }

    cout << ans << endl;

    return 0;
}