Skip to content

Splay 学习笔记

笔记约 5.1 千字
# 数据结构 # 平衡树 # Splay
检测到 KaTeX 加载失败，可能会导致文中的数学公式无法正常渲染。

Splay 是一种二叉查找树，它通过不断将某个节点旋转到根节点，使得整棵树仍然满足二叉查找树的性质，并且保持平衡而不至于退化为链。它可以在 O(log⁡n)O(\log n) 的时间内完成基于 Splay 操作的修改与查询。

本文提供使用原生指针和数组模拟指针两种方法实现的代码，可以点击代码块上方的切换按钮查看两种不同版本的代码。

#辅助函数 / 类

#node 结构体

以下为每个 Splay 节点的定义。

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
struct node {
    int value;
    node *lchild, *rchild, *parent, **root;
    size_t size, count;

    node()
        : value(0), lchild(nullptr), rchild(nullptr), parent(nullptr), root(nullptr), size(0), count(0) {}

    node(const int &_value, node *_parent, node **_root)
        : value(_value), lchild(nullptr), rchild(nullptr), parent(_parent), root(_root), size(1), count(1) {}

    ~node() {
        if (lchild != nullptr) delete lchild;
        if (rchild != nullptr) delete rchild;
    }
};

节点中的 root 表示指向根节点的指针的指针。这样做可以方便从任意一个节点找到整棵 Splay 的根节点，并修改它。

size 表示以当前节点为根的 Splay 共有多少个节点（包括自身），有了 size，就可以轻松地实现选择和排名操作。

此处在 node 的析构函数中递归释放所有内存以避免内存泄漏。

1
2
3
4
5
6
7
8
9
10
struct node {
    size_t l, r, f, c, s;
    int v;

    node()
        : l(0), r(0), f(0), c(0), s(0), v(0) {}

    node(T _v, size_t _f)
        : l(0), r(0), f(_f), c(1), s(1), v(_v) {}
};

s 表示以当前节点为根的 Splay 共有多少个节点（包括自身），有了它就可以轻松地实现选择和排名操作。

#关系（relation） / 儿子（child）

为了旋转操作的方便，我们给每个节点设置一个「关系」属性，表示该节点与其父节点的关系，若该节点为左孩子，则「关系」为 0，反之则为 1。relation() 方法用来计算这个「关系」，而 child() 方法返回与该节点「关系」为 x 的子节点的引用。

1
2
3
4
5
6
7
8
node *&child(unsigned int x) {
    return !x ? lchild : rchild;
}

unsigned relation() const {
    // 如果当前节点是其父亲节点的左儿子则返回 0，否则返回 1
    return this == parent->lchild ? 0 : 1;
}
1
2
3
4
5
6
7
8
9
10
11
12
13
14
struct node {
    // ...

    size_t &child(unsigned x) {
        return !x ? l : r;
    }

    // ...
};

unsigned relation(const size_t &u) {
    // 如果当前节点是其父亲节点的左儿子则返回 0，否则返回 1
    return u == tr[tr[u].f].l ? 0 : 1;
}

#上传信息（pushup）

易错：不要忘记加上 count。

1
2
3
void pushup() {
    size = lsize() + count + rsize();
}
1
2
3
inline void pushup(const size_t &u) {
    tr[u].s = tr[tr[u].l].s + tr[tr[u].r].s + tr[u].c;
}

#主要操作

#旋转（rotate）

为了使 Splay 保持平衡而进行旋转操作，旋转的本质是将某个节点上移一个位置。

旋转需要保证：

  • 整棵 Splay 的中序遍历不变（不能破坏二叉查找树的性质）。
  • 受影响的节点维护的信息依然正确有效。
  • root 必须指向旋转后的根节点。

在 Splay 中旋转分为两种：左旋和右旋。

以左旋（当前节点为父节点的左儿子为例），旋转分为三个步骤：

  1. 将祖父节点与自身连接；
  2. 将自己的右孩子接到自己的父节点的左孩子的位置（替代自己）；
  3. 将父节点接到自己的右孩子的位置。

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
void rotate() {
    // 旧的父节点
    node *old = parent;

    // 当前节点与父节点的关系
    unsigned x = relation();

    // 当前节点 <-> 父节点的父节点
    if (old->parent != nullptr) {
        old->parent->child(old->relation()) = this;
    }
    parent = old->parent;

    // 原先的另一个子节点 <-> 父节点
    if (child(x ^ 1) != nullptr) {
        child(x ^ 1)->parent = old;
    }
    old->child(x) = child(x ^ 1);

    // 原先的父节点 -> 子节点
    child(x ^ 1) = old;
    old->parent = this;

    // 更新节点信息
    old->pushup();
    pushup();
}
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
void rotate(size_t u) {
    // 旧的父节点
    size_t p = tr[u].f;

    // 当前节点与父节点之间的关系
    unsigned x = relation(u);

    // 当前节点 <-> 父节点的父节点
    if (tr[p].f) {
        tr[tr[p].f].child(relation(p)) = u;
    }
    tr[u].f = tr[p].f;

    // 原先的另一个子节点 <-> 父节点
    if (tr[u].child(x ^ 1)) {
        tr[tr[u].child(x ^ 1)].f = p;
    }
    tr[p].child(x) = tr[u].child(x ^ 1);

    // 原先的父节点 -> 子节点
    tr[u].child(x ^ 1) = p;
    tr[p].f = u;

    // 更新节点信息
    pushup(p);
    pushup(u);
}

#Splay

Splay 规定：每访问一个节点后都要强制将其旋转到根节点。此时旋转操作具体分为 6 种情况讨论（其中 xx 为需要旋转到根的节点）

  1. 如果 xx 的父亲是根节点，直接将 xx 左旋或右旋（图 1, 2）。

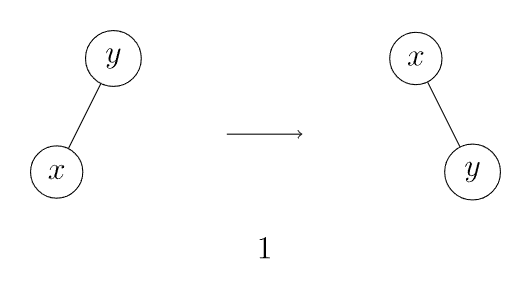
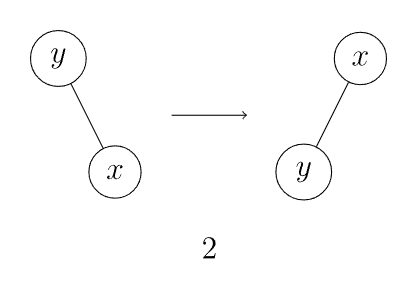
  2. 如果 xx 的父亲不是根节点，且 xx 和父亲节点的「关系」和父亲和父亲的父亲节点的「关系」相同，首先将其父亲左旋或右旋，然后将 xx 右旋或左旋（图 3, 4）。

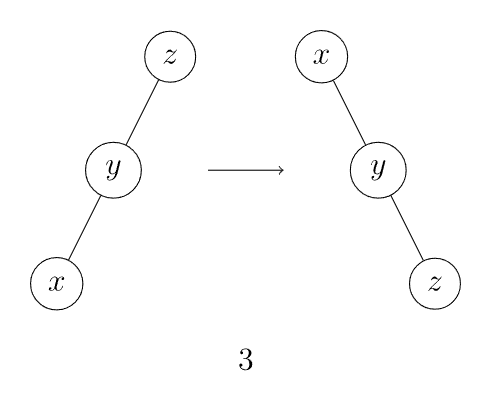
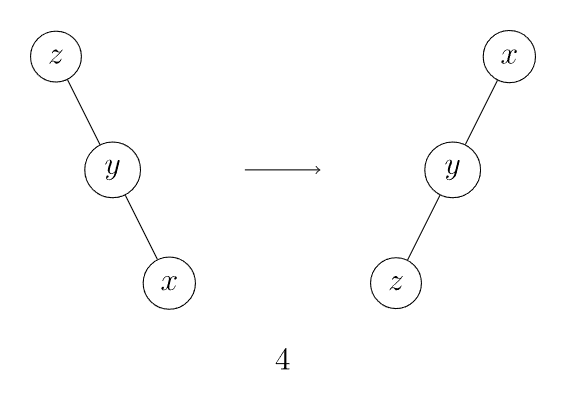
  3. 如果 xx 的父亲不是根节点，且 xx 和父亲节点的「关系」和父亲和父亲的父亲节点的「关系」不同，将 xx 左旋再右旋、或者右旋再左旋（图 5, 6）。

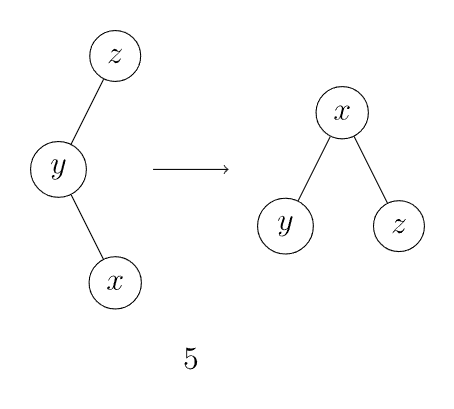
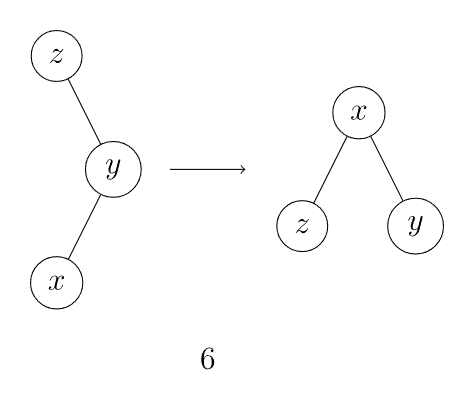
如果 Splay 操作的目标为 nullptr 则更新根节点。

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
// 旋转到给定的位置（target），默认行为为旋转为根节点
void splay(node *target = nullptr) {
    while (parent != target) {           // 父节点不是目标节点
        if (parent->parent == target) {  // 祖父节点是目标节点
            rotate();
        } else if (relation() == parent->relation()) {  // 关系相同
            parent->rotate();
            rotate();
        } else {
            rotate();
            rotate();
        }
    }

    // 更新根节点
    if (target == nullptr) *root = this;
}
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
// 旋转到给定的位置（target），默认行为为旋转为根节点
void splay(size_t u, size_t t = 0) {
    while (tr[u].f != t) {
        if (tr[tr[u].f].f == t) {
            rotate(u);
        } else if (relation(u) == relation(tr[u].f)) {
            rotate(tr[u].f);
            rotate(u);
        } else {
            rotate(u);
            rotate(u);
        }
    }

    // 更新根节点
    if (!t) root = u;
}

#插入（insert）

根据 BST 的性质二分查找插入即可。

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
node *_insert(const int &value) {
    node **target = &root, *parent = nullptr;

    while (*target != nullptr && (*target)->value != value) {
        parent = *target;
        parent->size++;

        // 根据大小向左右子树迭代
        if (value < parent->value) {
            target = &parent->lchild;
        } else {
            target = &parent->rchild;
        }
    }

    if (*target == nullptr) {
        *target = new node(value, parent, &root);
    } else {  // 存在现有节点直接修改节点信息即可
        (*target)->count++;
        (*target)->size++;  // 易忘：修改节点信息后需要更新节点大小
    }

    (*target)->splay();

    return root;
}
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
size_t _insert(const int &v) {
    size_t u = root, f = 0;

    while (u && tr[u].v != v) {
        f = u;
        // 根据数值大小向左右子树迭代
        u = v < tr[u].v ? tr[u].l : tr[u].r;
    }

    if (u) {
        tr[u].c++;
        tr[u].s++;  // 易忘：修改节点信息后需要更新节点大小
    } else {
        tr[u = ++cnt] = node(v, f);
        if (f) tr[f].child(v > tr[f].v) = u;  // 易忘：更新父节点信息
    }

    splay(u);

    return root;
}

为了下文操作中的方便，在建树时可以预先插入两个哨兵节点以防越界。

#查找（find）

同样地，根据 BST 的性质二分查找即可。

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
// 查找指定的值对应的节点
node *find(const int &value) {
    node *node = root;  // 从根节点开始查找

    while (node != nullptr && value != node->value) {
        // 根据数值大小向左右子树迭代
        node = value < node->value ? node->lchild : node->rchild;
    }

    if (node != nullptr) {
        node->splay();
    }

    return node;
}
1
2
3
4
5
6
7
8
9
10
11
12
size_t _find(const int &v) {
    size_t u = root;

    while (u && tr[u].v != v) {
        // 根据数值大小向左右子树迭代
        u = v < tr[u].v ? tr[u].l : tr[u].r;
    }

    if (u) splay(u);

    return u;
}

#排名（rank）

排名函数返回树中比给定值小的数的个数。

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
unsigned rank(const int &value) {
    node *node = find(value);

    if (node == nullptr) {  // 不存在则插入一个方便查找
        node = _insert(value);
        // 此时 node 已经成为根节点，直接计算即可
        unsigned res = node->lsize();  // 由于「哨兵」的存在，此处无需 -1
        erase(node);

        return res;
    }

    // 此时 node 已经成为根节点，直接计算即可
    return node->lsize();
}
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
unsigned rank(const int &v) {
    size_t u = _find(v);

    if (!u) {  // 不存在则插入一个方便查找
        u = _insert(v);

        // 此时 u 已经成为根节点，直接取左子树大小即可
        unsigned r = tr[tr[u].l].s;

        _erase(u);

        return r;
    }

    return tr[tr[u].l].s;
}

#选择（select）

选择函数返回树中第 kk 大的元素。传入的 kk 应保证不大于树中元素个数。

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
const int &select(unsigned k) {
    node *node = root;

    while (k < node->lsize() || k >= node->lsize() + node->count) {
        if (k < node->lsize()) {  // 所需的节点在左子树中
            node = node->lchild;
        } else {
            k -= node->lsize() + node->count;
            node = node->rchild;
        }
    }

    node->splay();

    return node->value;
}
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
const int &select(unsigned k) {
    size_t u = root;

    while (k < tr[tr[u].l].s || k >= tr[tr[u].l].s + tr[u].c) {
        if (k < tr[tr[u].l].s) {
            u = tr[u].l;
        } else {
            k -= tr[tr[u].l].s + tr[u].c;
            u = tr[u].r;
        }
    }

    splay(u);

    return tr[u].v;
}

#节点的前驱（predecessor）和后继（successor）

由 BST 的性质，前驱为左子树中最靠右的节点，后继为右子树中最靠左的节点。

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
// 前驱
//
// 左子树的最右点
node *predecessor() {
    node *pred = lchild;

    while (pred->rchild != nullptr) {
        pred = pred->rchild;
    }

    return pred;
}

// 后继
//
// 右子树的最左点
node *successor() {
    node *succ = rchild;

    while (succ->lchild != nullptr) {
        succ = succ->lchild;
    }

    return succ;
}
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
// 前驱
//
// 左子树的最右点
size_t _predecessor(const size_t &u) {
    size_t cur = tr[u].l;

    while (tr[cur].r) {
        cur = tr[cur].r;
    }

    return cur;
}

// 后继
//
// 右子树的最左点
size_t _successor(const size_t &u) {
    size_t cur = tr[u].r;

    while (tr[cur].l) {
        cur = tr[cur].l;
    }

    return cur;
}

#值的前驱（predecessor）和后继（successor）

使用 find() 函数找到对应的节点，再查询节点的前驱与后继即可。如果不存在则新建一个节点来辅助查询。

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
// 前驱
const int &predecessor(const int &value) {
    node *node = find(value);

    if (node == nullptr) {
        node = _insert(value);
        const int &result = node->predecessor()->value;
        erase(node);
        return result;
    }

    return node->predecessor()->value;
}

// 后继
const int &successor(const int &value) {
    node *node = find(value);

    if (node == nullptr) {
        node = _insert(value);
        const int &result = node->successor()->value;
        erase(node);
        return result;
    }

    return node->successor()->value;
}
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
// 前驱
const int &predecessor(const int &v) {
    size_t u = _find(v);

    if (!u) {  // 不存在则插入一个方便查找
        u = _insert(v);
        const int &r = tr[_predecessor(u)].v;
        _erase(u);  // 删除
        return r;
    }

    return tr[_predecessor(u)].v;
}

// 后继
const int &successor(const int &v) {
    size_t u = _find(v);

    if (!u) {  // 不存在则插入一个方便查找
        u = _insert(v);

        const int &r = tr[_successor(u)].v;

        _erase(u);  // 删除

        return r;
    }

    return tr[_successor(u)].v;
}

#删除（erase）

如果该节点上有多个相同的值，删除其中一个即可。否则删除节点。

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
// 删除节点
void erase(node *u) {
    if (u == nullptr) return;

    if (u->count > 1) {  // 存在重复的数
        u->splay();
        u->count--;
        u->size--;

        return;
    }

    node *pred = u->predecessor(),
          *succ = u->successor();

    pred->splay();      // 将前驱旋转到根节点
    succ->splay(pred);  // 将后继旋转到根节点的右儿子

    delete succ->lchild;  // 此时要删的节点为根节点的左儿子且为叶子节点
    succ->lchild = nullptr;

    // 更新节点信息
    succ->pushup();
    pred->pushup();
}

// 删除值
void erase(const int &value) {
    erase(find(value));
}
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
// 删除节点
void _erase(size_t u) {
    if (!u) return;

    if (tr[u].c > 1) {  // 存在重复的数
        splay(u);
        tr[u].c--;
        tr[u].s--;

        return;
    }

    size_t pred = _predecessor(u),
            succ = _successor(u);

    splay(pred);        // 将前驱旋转到根节点
    splay(succ, pred);  // 将后继旋转到根节点的右儿子

    tr[succ].l = 0;  // 此时要删的节点为根节点的左儿子且为叶子节点

    // 更新节点信息
    pushup(succ);
    pushup(pred);
}

// 删除值
void erase(const int &v) {
    _erase(_find(v));
}

#代码

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
71
72
73
74
75
76
77
78
79
80
81
82
83
84
85
86
87
88
89
90
91
92
93
94
95
96
97
98
99
100
101
102
103
104
105
106
107
108
109
110
111
112
113
114
115
116
117
118
119
120
121
122
123
124
125
126
127
128
129
130
131
132
133
134
135
136
137
138
139
140
141
142
143
144
145
146
147
148
149
150
151
152
153
154
155
156
157
158
159
160
161
162
163
164
165
166
167
168
169
170
171
172
173
174
175
176
177
178
179
180
181
182
183
184
185
186
187
188
189
190
191
192
193
194
195
196
197
198
199
200
201
202
203
204
205
206
207
208
209
210
211
212
213
214
215
216
217
218
219
220
221
222
223
224
225
226
227
228
229
230
231
232
233
234
235
236
237
238
239
240
241
242
243
244
245
246
247
248
249
250
251
252
253
254
255
256
257
258
259
260
261
262
263
264
265
266
267
268
269
270
271
272
273
274
275
276
277
278
279
#include <limits>

template <typename T>
class Splay {
  private:
    struct node {
        T value;
        node *lchild, *rchild, *parent, **root;
        size_t size, count;

        node()
            : value(0), lchild(nullptr), rchild(nullptr), parent(nullptr), root(nullptr), size(0), count(0) {}

        node(const T &_value, node *_parent, node **_root)
            : value(_value), lchild(nullptr), rchild(nullptr), parent(_parent), root(_root), size(1), count(1) {}

        ~node() {
            if (lchild != nullptr) delete lchild;
            if (rchild != nullptr) delete rchild;
        }

        node *&child(unsigned int x) {
            return !x ? lchild : rchild;
        }

        unsigned relation() const {
            // 如果当前节点是其父亲节点的左儿子则返回 0，否则返回 1
            return this == parent->lchild ? 0 : 1;
        }

        // 左儿子大小
        size_t lsize() const {
            return lchild == nullptr ? 0 : lchild->size;
        }

        // 右儿子大小
        size_t rsize() const {
            return rchild == nullptr ? 0 : rchild->size;
        }

        // 上传信息
        void pushup() {
            size = lsize() + count + rsize();
        }

        // 旋转
        void rotate() {
            // 旧的父节点
            node *old = parent;

            // 当前节点与父节点的关系
            unsigned x = relation();

            // 当前节点 <-> 父节点的父节点
            if (old->parent != nullptr) {
                old->parent->child(old->relation()) = this;
            }
            parent = old->parent;

            // 原先的另一个子节点 <-> 父节点
            if (child(x ^ 1) != nullptr) {
                child(x ^ 1)->parent = old;
            }
            old->child(x) = child(x ^ 1);

            // 原先的父节点 -> 子节点
            child(x ^ 1) = old;
            old->parent = this;

            // 更新节点信息
            old->pushup();
            pushup();
        }

        // Splay
        //
        // 旋转到给定的位置（target），默认行为为旋转为根节点
        void splay(node *target = nullptr) {
            while (parent != target) {           // 父节点不是目标节点
                if (parent->parent == target) {  // 祖父节点是目标节点
                    rotate();
                } else if (relation() == parent->relation()) {  // 关系相同
                    parent->rotate();
                    rotate();
                } else {
                    rotate();
                    rotate();
                }
            }

            // 更新根节点
            if (target == nullptr) *root = this;
        }

        // 前驱
        //
        // 左子树的最右点
        node *predecessor() {
            node *pred = lchild;

            while (pred->rchild != nullptr) {
                pred = pred->rchild;
            }

            return pred;
        }

        // 后继
        //
        // 右子树的最左点
        node *successor() {
            node *succ = rchild;

            while (succ->lchild != nullptr) {
                succ = succ->lchild;
            }

            return succ;
        }
    } * root;

    // 插入（内部函数）
    node *_insert(const T &value) {
        node **target = &root, *parent = nullptr;

        while (*target != nullptr && (*target)->value != value) {
            parent = *target;
            parent->size++;

            // 根据大小向左右子树迭代
            if (value < parent->value) {
                target = &parent->lchild;
            } else {
                target = &parent->rchild;
            }
        }

        if (*target == nullptr) {
            *target = new node(value, parent, &root);
        } else {  // 存在现有节点直接修改节点信息即可
            (*target)->count++;
            (*target)->size++;  // 易忘：修改节点信息后需要更新节点大小
        }

        (*target)->splay();

        return root;
    }

    // 查找指定的值对应的节点
    node *find(const T &value) {
        node *node = root;  // 从根节点开始查找

        while (node != nullptr && value != node->value) {
            if (value < node->value) {
                node = node->lchild;
            } else {
                node = node->rchild;
            }
        }

        if (node != nullptr) {
            node->splay();
        }

        return node;
    }

    // 删除
    void erase(node *u) {
        if (u == nullptr) return;

        if (u->count > 1) {  // 存在重复的数
            u->splay();
            u->count--;
            u->size--;

            return;
        }

        node *pred = u->predecessor(),
             *succ = u->successor();

        pred->splay();      // 将前驱旋转到根节点
        succ->splay(pred);  // 将后继旋转到根节点的右儿子

        delete succ->lchild;  // 此时要删的节点为根节点的左儿子且为叶子节点
        succ->lchild = nullptr;

        // 更新节点信息
        succ->pushup();
        pred->pushup();
    }

  public:
    Splay()
        : root(nullptr) {
        // 哨兵节点
        insert(std::numeric_limits<T>::min());
        insert(std::numeric_limits<T>::max());
    }

    ~Splay() {
        delete root;
    }

    // 插入
    void insert(const T &value) {
        _insert(value);
    }

    // 删除
    void erase(const T &value) {
        erase(find(value));
    }

    // 排名
    unsigned rank(const T &value) {
        node *node = find(value);

        if (node == nullptr) {
            node = _insert(value);
            // 此时 node 已经成为根节点，直接计算即可
            int res = node->lsize();  // 由于「哨兵」的存在，此处无需 -1
            erase(node);

            return res;
        }

        // 此时 node 已经成为根节点，直接计算即可
        return node->lsize();
    }

    // 选择
    const T &select(unsigned k) {
        node *node = root;

        while (k < node->lsize() || k >= node->lsize() + node->count) {
            if (k < node->lsize()) {  // 所需的节点在左子树中
                node = node->lchild;
            } else {
                k -= node->lsize() + node->count;
                node = node->rchild;
            }
        }

        node->splay();

        return node->value;
    }

    // 前驱
    const T &predecessor(const T &value) {
        node *node = find(value);

        if (node == nullptr) {
            node = _insert(value);
            const T &result = node->predecessor()->value;
            erase(node);
            return result;
        }

        return node->predecessor()->value;
    }

    // 后继
    const T &successor(const T &value) {
        node *node = find(value);

        if (node == nullptr) {
            node = _insert(value);
            const T &result = node->successor()->value;
            erase(node);
            return result;
        }

        return node->successor()->value;
    }
};
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
71
72
73
74
75
76
77
78
79
80
81
82
83
84
85
86
87
88
89
90
91
92
93
94
95
96
97
98
99
100
101
102
103
104
105
106
107
108
109
110
111
112
113
114
115
116
117
118
119
120
121
122
123
124
125
126
127
128
129
130
131
132
133
134
135
136
137
138
139
140
141
142
143
144
145
146
147
148
149
150
151
152
153
154
155
156
157
158
159
160
161
162
163
164
165
166
167
168
169
170
171
172
173
174
175
176
177
178
179
180
181
182
183
184
185
186
187
188
189
190
191
192
193
194
195
196
197
198
199
200
201
202
203
204
205
206
207
208
209
210
211
212
213
214
215
216
217
218
219
220
221
222
223
224
225
226
227
228
229
230
231
232
233
234
235
236
237
238
239
240
241
242
243
244
245
246
247
248
249
250
251
252
253
254
#include <limits>

template <typename T>
class Splay {
  private:
    size_t root, cnt;

    struct node {
        size_t l, r, f, c, s;
        T v;

        node()
            : l(0), r(0), f(0), c(0), s(0), v(0) {}

        node(T _v, size_t _f)
            : l(0), r(0), f(_f), c(1), s(1), v(_v) {}

        size_t &child(unsigned x) {
            return !x ? l : r;
        }
    } tr[N];

    // 上传信息
    inline void pushup(const size_t &u) {
        tr[u].s = tr[tr[u].l].s + tr[tr[u].r].s + tr[u].c;
    }

    // 节点关系
    unsigned relation(const size_t &u) {
        // 如果当前节点是其父亲节点的左儿子则返回 0，否则返回 1
        return u == tr[tr[u].f].l ? 0 : 1;
    }

    void rotate(size_t u) {
        // 旧的父节点
        size_t p = tr[u].f;

        // 当前节点与父节点之间的关系
        unsigned x = relation(u);

        // 当前节点 <-> 父节点的父节点
        if (tr[p].f) {
            tr[tr[p].f].child(relation(p)) = u;
        }
        tr[u].f = tr[p].f;

        // 原先的另一个子节点 <-> 父节点
        if (tr[u].child(x ^ 1)) {
            tr[tr[u].child(x ^ 1)].f = p;
        }
        tr[p].child(x) = tr[u].child(x ^ 1);

        // 原先的父节点 -> 子节点
        tr[u].child(x ^ 1) = p;
        tr[p].f = u;

        // 更新节点信息
        pushup(p);
        pushup(u);
    }

    // Splay
    //
    // 旋转到给定的位置（target），默认行为为旋转为根节点
    void splay(size_t u, size_t t = 0) {
        while (tr[u].f != t) {
            if (tr[tr[u].f].f == t) {
                rotate(u);
            } else if (relation(u) == relation(tr[u].f)) {
                rotate(tr[u].f);
                rotate(u);
            } else {
                rotate(u);
                rotate(u);
            }
        }

        // 更新根节点
        if (!t) root = u;
    }

    // 前驱
    //
    // 左子树的最右点
    size_t _predecessor(const size_t &u) {
        size_t cur = tr[u].l;

        while (tr[cur].r) {
            cur = tr[cur].r;
        }

        return cur;
    }

    // 后继
    //
    // 右子树的最左点
    size_t _successor(const size_t &u) {
        size_t cur = tr[u].r;

        while (tr[cur].l) {
            cur = tr[cur].l;
        }

        return cur;
    }

    size_t _find(const T &v) {
        size_t u = root;

        while (u && tr[u].v != v) {
            // 根据数值大小向左右子树迭代
            u = v < tr[u].v ? tr[u].l : tr[u].r;
        }

        if (u) splay(u);

        return u;
    }

    size_t _insert(const T &v) {
        size_t u = root, f = 0;

        while (u && tr[u].v != v) {
            f = u;
            // 根据数值大小向左右子树迭代
            u = v < tr[u].v ? tr[u].l : tr[u].r;
        }

        if (u) {
            tr[u].c++;
            tr[u].s++;
        } else {
            tr[u = ++cnt] = node(v, f);
            if (f) tr[f].child(v > tr[f].v) = u;
        }

        splay(u);

        return root;
    }

    void _erase(size_t u) {
        if (!u) return;

        if (tr[u].c > 1) {  // 存在重复的数
            splay(u);
            tr[u].c--;
            tr[u].s--;

            return;
        }

        size_t pred = _predecessor(u),
               succ = _successor(u);

        splay(pred);        // 将前驱旋转到根节点
        splay(succ, pred);  // 将后继旋转到根节点的右儿子

        tr[succ].l = 0;  // 此时要删的节点为根节点的左儿子且为叶子节点

        // 更新节点信息
        pushup(succ);
        pushup(pred);
    }

  public:
    Splay()
        : root(0), cnt(0) {
        // 插入哨兵节点
        insert(std::numeric_limits<T>::min());
        insert(std::numeric_limits<T>::max());
    }

    // 插入
    void insert(const T &v) {
        _insert(v);
    }

    // 删除
    void erase(const T &v) {
        _erase(_find(v));
    }

    // 排名
    unsigned rank(const T &v) {
        size_t u = _find(v);

        if (!u) {  // 不存在则插入一个方便查找
            u = _insert(v);

            // 此时 u 已经成为根节点，直接取左子树大小即可
            unsigned r = tr[tr[u].l].s;

            _erase(u);

            return r;
        }

        return tr[tr[u].l].s;
    }

    // 选择
    const T &select(unsigned k) {
        size_t u = root;

        while (k < tr[tr[u].l].s || k >= tr[tr[u].l].s + tr[u].c) {
            if (k < tr[tr[u].l].s) {
                u = tr[u].l;
            } else {
                k -= tr[tr[u].l].s + tr[u].c;
                u = tr[u].r;
            }
        }

        splay(u);

        return tr[u].v;
    }

    // 前驱
    const T &predecessor(const T &v) {
        size_t u = _find(v);

        if (!u) {  // 不存在则插入一个方便查找
            u = _insert(v);

            const T &r = tr[_predecessor(u)].v;

            _erase(u);  // 删除

            return r;
        }

        return tr[_predecessor(u)].v;
    }

    // 后继
    const T &successor(const T &v) {
        size_t u = _find(v);

        if (!u) {  // 不存在则插入一个方便查找
            u = _insert(v);

            const T &r = tr[_successor(u)].v;

            _erase(u);  // 删除

            return r;
        }

        return tr[_successor(u)].v;
    }
};

#参考资料

  1. Splay 学习笔记（一），黄浩睿，2015 年 12 月 20 日。
  2. Splay，OI Wiki，2022 年 3 月 20 日。